|
SUNDAY EDITION December 28th, 2025 |
|
Home :: Archives :: Contact |
 |
Economics and Nuclear Energy: A Long Modern SurveyProfessor Ferdinand E. Banksferdinand.banks@telia.com May 28th, 2009 Abstract: This survey extends a topic I briefly discussed during my recent course at the Asian Institute of Technology (AIT). Special attention is occasionally paid Sweden, because mainstream academic economics is focused on optimal arrangements, and this once described the Swedish nuclear sector, where the cost of nuclear-based power may still be the lowest in the world. Just as significant, for over a decade politically motivated efforts to eliminate nuclear as an energy mainstay have not been successful. Many observations below have appeared in my energy economics textbook (2007), however the structure of the present paper was motivated by the many valuable discussions on nuclear matters in the forum EnergyPulse (www.energypulse.net). A fundamental contention in this article is that a new energy economy must eventually be brought into existence, and this new economy would probably be sub-optimal without an expanded nuclear component (as well as many new renewables). Some mathematics appears in this exposition, but much of it can be ignored if it makes the reader uncomfortable.
Key Terms: Load Division, capital cost, nuclear fuel cycle, renewables
1. INTRODUCTION
As is well known, nuclear energy is not a popular medium with everybody. Even in France, virtually the capital of ‘the peaceful atom’, there are many persons who hope that someday another energy source will replace all or a large part of the almost 80 percent of the electricity supply that originates with nuclear. Frankly, even if there were a major accident in France, or a nearby country, that yearning seems unrealistic. In countries like France and Japan, where adequate energy is recognized as indispensable for maintaining economic competitiveness, the present energy configurations have never been seriously questioned. ‘No oil, no gas, no coal, no choice’ is the way the French put it, and although the energy prospects of many other countries may appear to be rosier, they could find themselves warbling the same melancholy tune some day. This does not mean however that it makes economic sense to consign conservation, renewables and/or other non-conventional (or alternative) energy sources and strategies to the margins of the energy scene. The ugly fact of the matter is that the world would probably be in a very bad way if these things do not become widely available in a few decades, or perhaps even sooner, because they might have to accommodate a very large part of the energy load in all except a few lucky countries. But one way to make sure that they will not be available is for a majority of the voters in a given country, or even a decisive sub-set of the voters, or for that matter just the decision-makers to accept the twisted hypothesis that it is economical to introduce these items on a large scale before present and future costs and other constraints are fully understood. When I say future costs I am thinking of how a rising price of e.g. oil and gas, as well as governmental policies concerning carbon emissions, will influence the present (opportunity) cost of nuclear. An example involving nuclear equipment might be useful here. The most widely used nuclear power generator today is the light-water reactor (LWR), so named as to distinguish it from the heavy water or deuterium oxide technology emphasized in Canada. (There is a short glossary in the appendix that is intended to clarify this terminology!) These reactors, their predecessors, and various ‘spin-offs’ are generally labelled first and second generation models. The most modern equipment available today however are the third generation models, such as the recently designated ‘Evolutionary Pressurised Reactor’, which was originally developed by France and called the European Pressurised Reactor (EPR). The intention with this reactor is to achieve an unconditional safety, in that ‘melt-downs’ cannot take place. (If control systems stop working, the reactor is supposed to shut down automatically, dissipate the heat produced by the reactions in its core, and prevent both fuel and radioactive waste from escaping.) One of these reactors – the largest in the world (at 1600 megawatts = 1600 MW) – is being constructed in Finland, and is designated Olkiluoto 3. Given the costly delays that have been experienced, and the high efficiency of existing Finnish reactors, a question could be asked as to whether, at the present time, it might have made more economic sense to construct two more LWRs (instead of Olkiluoto 3) if the same capacity was desired, taking special care to incorporate the latest technological attributes into these reactors. It is possible that a study of relative costs by Guentcheva and Vira (1984) of the Technical Research Centre (Helsinki, Finland) was important in convincing Finnish decision makers that there were substantial economic advantages of an increasing returns to scale nature to be gained by constructing a very large reactor. The equation they suggest as relevant in these matters and especially applicable to Finnish conditions is [(specific cost 1)/(specific cost 2) = (size 1)/size 2)m-1], where the values of m ranged from 0.38 to 0.75. On the basis of some empirical work by C.M. Held (1983) it appears that this equation is fairly useful, however its applicability to what is largely a new technological situation, where a number of things can go wrong for non-engineering reasons, is uncertain. At the same time it should be appreciated that had construction followed the conjectured plan, with ‘ground break’ taking place in 2005 and ‘grid power’ achieved in 2009, Olkiluoto 3 could be labelled a very profitable enterprise – except of course by members of the anti-nuclear booster club. The opinion here is that even with the unexpected increase in expense due to an increased construction time, in the long-run the Finns will be grateful for the presence of this equipment, and I have been informed that still another of these (Gen 3) reactors may be constructed.. It has also been claimed that a fourth generation reactor is not many years away. This kind of reactor will feature much higher temperatures, which in turn would raise the reactor efficiency by a large amount. It could therefore be suggested that faced with an increased rate of depletion of oil and natural gas, the energy strategy employed by Switzerland during World War Two – which featured a very high degree of electrification of the entire economy – should be given careful consideration by energy-intensive countries. It has been estimated by the German firm Siemens that there will be 400 new reactors in the world by 2030, although it is impossible at the present time to reckon their size and technological details. Siemens just announced that it will join the Russian firm Rosatom for the purpose of developing and selling Rosatom’s pressurized water reactor, particularly in Russia, China, India and Bulgaria. In 2008 construction began on two new reactors in Russia, which should be good news for Germany and several other countries, because it could increase the availability of natural gas for Russia’s gas customers. The early theorists of Soviet communism seemed to believe that Soviet power plus electricity would create a heaven on earth. Similarly, the implicit assumption in Sweden after the Social Democrats assumed power was that something called the ‘Swedish welfare state’ would emphasize social democracy plus electricity. A low level statistical analysis and a simple algebraic demonstration makes it clear that in terms of reliability and cost, the Swedish nuclear sector was the most efficient in the world before the curse of (electric) deregulation arrived. It is due to an intensified concern for the economic future that the irrational nuclear ‘downsizing’ in this country (Sweden) has been at least temporarily halted. The key departure was upgrading the ten remaining reactors so that they could produce the same electric energy (in kilowatt-hours = kWh) as the original twelve reactors, which amounts to nearly 47 percent of the total generated energy. (Approximately the same amount is accounted for by hydro.) The logic here is straightforward, and cannot be altered by the resolute ignoring or disparaging of mainstream economic history: a high electric intensity for firms, combined with a high rate of industrial investment and the technological skill created by a modern educational system, will lead to a high productivity for large and small businesses. This in turn results in a steady increase in employment, real incomes, and the most important ingredients of social security (such as pensions and comprehensive health care). This is exactly what happened, and a relevant question of late is whether a once magnificent welfare ‘structure’ that – for a number of years – was a roll model for the residents and politicians of many countries, can be kept afloat if some of the most modern electric generating facilities in the world are scrapped for short-term political considerations. For instance, in order to recruit supporters with anti-nuclear tendencies, the recent Social Democratic prime minister informed actual and potential voters who prefer opinion and feelings to evidence and logic that nuclear power was “obsolete”. As it happens, this judgement was the opposite of the truth. The Nobel laureate Dennis Gabor once called the nuclear reactor the most important scientific invention of the 20th Century, and its further development should make it one of the most important implements of the present century. In the light of human needs and desires, few energy sources have more to offer than the reliable and comparatively inexpensive electricity that might be made available when the next generation (or generations) of nuclear equipment comes into being. For some obscure reason, in l978 all the major political parties in Sweden agreed that the growing controversy over the future of nuclear energy should be settled by a national referendum. The electorate was subsequently asked to choose between nuclear acceptance, or the more-or-less immediate closing of as many nuclear facilities as possible, or a gradual phase-out that was to be complete by 2010. Confronted by a whirlwind of neurotic fictions launched by a technophobic nuclear opposition, the latter option was selected. Although not fully comprehended by most Swedes even now, a key factor in that pseudo-scientific travesty was an assumption that the rising prosperity of Sweden could be maintained even if the country’s nuclear assets were liquidated. In other words, the choice between nuclear energy and ‘something-else’ was reduced to a matter of taste, and to add insult to injury, the country’s energy assets were pictured by many politicians as having little or nothing to do with the macro-economy, although in point of truth they have everything to do with it. To a considerable extent, that ill-founded assumption is now passé, which is why a small majority of Swedish voters are no longer hostile to nuclear. In the UK, on the other hand, some polls indicate that many voters want to see nuclear and coal-based installations phased out in favour of renewables, while the UK government is in favour of a nuclear revival. This is because, as former Prime Minister Blair once observed while commenting on some environmental considerations, without such a departure it will be impossible to achieve large reductions in carbon dioxide (CO2) emissions. And not only Mr Blair. James Lovelock, a founder of Greenpeace, has surprisingly said that we do not need to fear nuclear energy, which he endorses as “the safest and most environmentally friendly source of that vital product, electricity.” No country has made as great an effort to include renewables in the energy mainstream as Sweden, but even so the result in terms of the energy now being generated is insignificant. Many Swedes now realize that while technically renewables can be substituted for nuclear, the benefit-cost ratio is economically unacceptable. The decision makers in the UK know this too, because much of their talk about environment derives from their concern about energy: if more nuclear is not provided, there will have to be a greatly increased resort to coal.
2. INTRODUCING CAPACITY FACTORS AND BASE LOADS:
Before going to some slightly more technical considerations, there is one aspect of the present debate about nuclear energy that everyone should consider. It turns on the expression Capacity Factor (CF), which has to do with the amount of energy that is actually produced over a given period as compared to the amount that could be produced if the facility had operated at maximum (or rated) output one-hundred percent of the time. This can be written CF = Actual Energy Output over a given period divided by Rated or Maximum Output. When you hear about the beauty of wind or solar energy, make sure that you ask about the Capacity Factor. Consider a wind turbine with a power rating of 100 kilowatts. In a month of 30 days its maximum energy output is 100 x 30 x 24 = 7,200 kilowatt-hours. However its measured output during that period would likely be lower, and perhaps much lower. Suppose it was 3,600 kilowatt hours. Then we would have CF = 3600/7200 = 0.50 = 50%. For wind a capacity factor of 15-35% appears average; and Jeffrey Michel confirms a stable 0.17 average for Germany before 2007, although it might have reached 0.2 in 2007. As for nuclear, 30 years ago capacity factors in the U.S. were about 55% due to the ‘down-time’ caused by unscheduled outages and scheduled maintenance, but now outages have decreased and average values are above 85%. Also, if capacity factors are calculated net of scheduled outages, then occasionally they are about 95%, which apparently applies to plants managed by e.g. Exelon. Now examine an important diagram.
Figure 1a is about the configuration of demand, with the story told on the basis of capacity. To be specific, the demand for electricity (or electric capacity) typically varies during a day (24 hours) in the cyclic pattern shown in Figure 1a. The load (on the vertical axis) is in kilowatts (kW), or megawatts (MW) or something of that nature (where ‘mega’ stands for millions). Here you can think in terms of the size and number of light bulbs in your residence, many of which are not on in the middle of the day, while all of them could be on in the evening. We might therefore say that your demand ‘peaks’ in the evening. On the horizontal axis in Figure 1a are hours, ranging from e.g. midnight to midnight – a 24 hour period. (Naturally we could have used a one month or one year period). Thus the ‘box’ that is designated “Base Load” is a portion of the energy that is expended during a 24 hour period, and this is measured in e.g. kilowatt hours (= kWh). The remainder of the energy for this period (in kWh) is the remainder of the area under this curve. Continuing with the light bulb example, you do not pay the firm that supplies you with electricity for the size of your light bulbs, but you pay them for the amount of electric energy you actually require and they provide, just as they pay the seller of e.g. coal or gas or ‘uranium’ for the items they use to produce electricity (and in which the energy resides in the first place). The base load here can be thought of as the load (in e.g. kW or MW) that is always on the line, while the peak load is the maximum load on the line, and which typically is in place for only a comparatively short period. A base load power plant is one that customarily provides a steady flow of power to a grid (i.e. a collection of power lines), and operates at all times except for unscheduled ‘down-time’ and scheduled maintenance. Clearly, few readers would deny that the base load ought to be ‘carried’ by extremely reliable equipment. They should also add the expressions base load and peak load to their vocabularies as soon as possible, especially if they would like to participate in influential discussions on the present topic as an equal rather than an interloper. In addition they should attempt to comprehend that we will not have much use for the highly stable demand curves featured in our courses in microeconomics. Figure 1b is one of this kind, and it unfortunately has a tendency to make appearances in important documents where it does not belong. Many readers probably understand that if generating equipment is extremely expensive – as is the case with a very large nuclear or coal power plant – it cannot be an optimal arrangement to allow it to stand idle during most of the day in order to be available during the period when there is a peak load to be serviced. Conventionally, nuclear, coal, hydro and – since the introduction of combined cycle equipment – gas have been important for the base load, while gas and to a certain extent hydro have been important for the peak load. I have also heard it claimed that small pebble-bed reactors may be constructed in the future that are capable of supplying economic peak-load power. In fact there is a claim that so-called mini-reactors employing this technology can be installed with no more effort or complexity than installing a large transformer. The beauty with this equipment is that it can be hermetically sealed and its power is available for 40 or 50 years. Some years ago, when I was in the U.S. Army, and for a short time stationed near Yokohama (Japan) in the vicinity of a small dam, I was able to get some insight into the functioning of a hydroelectric installation. One of the more interesting (informal) lectures I received on that occasion had to do with the unapparent flexibility of that facility, and just as interesting, the last time I visited Japan I was told that large dams are often capable of ‘returning’ well over than 50 times the energy invested in them – by which it is meant that if the money invested in constructing these dams were translated into energy units (which is a simple algebraic operation) and compared to the energy generated by these structures over their expected lifetimes, the ratio would be at least fifty. Only nuclear approaches this impressive result.
3. DEEPER MEANINGS
This section borrows from and extends some observations made in my short paper ‘SOME FRIENDLY ECONOMICS FOR THE NUCLEAR ENERGY BOOSTER CLUB’ (2008), which I took the liberty of circulating widely to many members of that club, as well as a number of ladies and gentlemen who were probably less than pleased to receive my humble opinions of nuclear energy or anything else. I also take this opportunity to provide a low-key discussion of several comments on that paper. But before doing that I would like to claim that perhaps the most straightforward reasoning in favour of nuclear-based electricity is in the non-technical article of Rhodes and Beller (2000). They say that “Because diversity and redundancy are important for safety and security, renewable energy sources ought to retain a place in the energy economy of the century to come.” The meaning here is clear, especially if you add that we probably will never possess what is known in intermediate economic theory as the optimal amount of nuclear power. Next they unambiguously state that “nuclear power should be central….Nuclear power is environmentally safe, practical and affordable. It is not the problem – it is one of the solutions.” Everyone of course does not welcome this kind of reminder. The construction of the Swedish nuclear sector and its later development was one of the most impressive engineering phenomena of the 20th century, however eventually a glib argument began to circulate that nuclear energy was just a “parenthesis” in world energy history, and a recent prime minister called nuclear “obsolete”. Just for the record, the Swedish nuclear sector – comprising 12 reactors, and supplying almost half of the Swedish electric power – was constructed in only 13 years. In the period, before electric deregulation gained momentum, the cost of electricity generated in Swedish nuclear facilities was among the lowest in the world – and occasionally the lowest. In addition, to my great surprise, I discovered that the Swedish electricity price was also extremely low. This was especially favourable for the Swedish industrial sector. In the most nuclear intensive country in the world – which is France – the intention from the beginning was to create a nuclear sector that would provide some of the lowest priced electricity in the world, and to use that electricity to make it possible for the country to optimize its macroeconomic performance. Unlike the situation in Sweden, the French decision makers made plans to stay in the forefront of nuclear development, and in addition to provide both the industrial and household sectors with reliable and comparatively inexpensive electricity. They also expressed a desire to achieve and maintain a low level of carbon emissions. Assuming that this is comprehensible, I would like to emphasize that nuclear cost issues need to be examined in greater detail for a meaningful discussion of electricity generation to take place. For France the basic comparison was between nuclear and coal, and given the various costs associated with importing and using coal, it was easy to show that nuclear was preferable. It might be possible to argue successfully that this is not true for the U.S., but I happen to skeptical. This issue cannot be treated at great length in the present paper, but my energy economics textbook (2007) presents a more detailed clarification. The core of my argument turns on the supply of reactor fuel, the length of ‘life’ of a reactor, the lack of carbon emissions, the possibility of a radical improvement in reactor technology and the time required to construct reactors (which is important for the investment cost, which in turn is important for the capital cost). Below I briefly consider this matter, while it is examined at considerable length in the mostly non-technical chapter on nuclear in my textbook. I can add that I always insist that my students should be able to distinguish between investment cost and capital cost. I have had the misfortune to see many estimates of the cost of a kilowatt of capacity of nuclear energy. Too many as far as I am concerned! They range from $1500/kW by the director of an electric generating firm, to $9000/kW by a gentleman who is convinced that most of my work on the economics of nuclear energy hardly deserves to be called nonsense. In my own calculations I often use $2500-3000/kW. In a similar vein, a (3rd Generation) reactor is being constructed in Finland at the present time that has a capacity of 1,600 megawatts (= 1600 MW), which makes it the largest in the world from the point of view of capacity, and initially the intention was to construct it in 5 years. An early estimate of its investment cost was 5 billion dollars. Now it appears that it will take 8 years to construct this reactor, and it has been claimed that before grid power is attained, its cost may reach 8 billion dollars, and perhaps slightly more. None of this bothers me, because although much of this depressing news originates with engineers who have a far more thorough knowledge of industrial management and engineering than I ever possessed, I am satisfied with my ability to examine the issue on the basis of economics and history. First of all we can consider the time from construction start to commercial operation of nuclear power plants in six important industrial countries. The figures that will be given below originate in the database of the International Atomic Energy Agency, and are quoted in an important article by Roques, Nuttall, Newbery, de Neufville and Connors (2006). I have also questioned Fabien Roques – who wrote the chapter on nuclear energy in the latest IEA survey – and he assures me that he finds them realistic. I quote them here employing the scheme [Country (Minimum Time, Maximum Time, Average Time)], where the times are of course construction times, and these are measured in years. China (4.5, 6.3, 5.1); France (4.9, 16.3, 7.1); Japan (3.3, 8,1, 4.7); Russia (2.1, 20.3, 6.8); UK (4.9, 23.5, 10.8); U.S. (3.4, 23.4, 9.2). In examining these it should be clear that the average times are weighted in terms of capacity (i.e. power) or energy. Worldwide, since l991, the figures given by Roques (et al) are (4.0, 8.0, 5.2). With an average construction time of 5.2 years, it might therefore be possible to argue that taking 8 or 9 years to construct a nuclear facility is an aberration, and in the fullness of time, the average plant will be constructed in about 5 years. My position of course is that once the nuclear renaissance get up steam, the average plant will be constructed in 4 years or less. As I informed someone in one of the forums to which I contribute, unlike most concerned citizens, I know what happened in e.g. the United States during the Second World War. The battle of Midway took place in l942, and in the approximately 3 years following that major naval clash until the end of the war, the United States constructed 17 fleet (i.e. large) aircraft carriers, 10 medium carriers, and 86 escort carriers. In addition crews and pilots were trained to efficiently and successful utilize these assets, and hundreds of other warships were produced. It should be appreciated that before the U.S. entered the war, nobody in their right mind would have claimed that the ‘miracles’ of modern technology and management skill that became commonplace during the war were possible. Another quantitative triumph was the U.S. armoured force, although techologically I regard it as deficient. The main U.S. battle tank, the Sherman, was produced in the thousands, even after it was discovered that it was an inferior piece of equipment. What is still not adequately understood is that it would have been extremely simple to produce in large numbers the qualitatively superior Pershing tank. Had that been done, and the approaches to the port of Antwerp cleared when they should have been cleared, American armor would have been across the Rhine and in Berlin before Christmas of 1944. I call this a gigantic failure to exploit existing technology, and the same kind of flaw applies to the inability to greatly reduce the time of construction of nuclear plants. According to Donald E. Carr in his brilliant book (1976), the Japanese were able to construct a nuclear plant in 4 years in the l970s, which leads me to believe that they will be able to construct one in 3 years when their decision makers and voters eventually comprehend what awaits their standard of living if they do not get the energy message. (I was also told some years ago in Vienna that the Japanese government is in no hurry to increase the size of the present nuclear inventory. What they want instead is to introduce breeder reactors, which would enable a greater utilization of the energy in a reactor’s fuel.) It might also be possible to argue that if at the present time if it takes 5 years or more to construct a nuclear plant, then coal is a more economic resource for electric generation than nuclear, but since I expect nuclear plants to eventually take less than 4 years to construct, this should not be the case. I can close this part of the exposition by pointing out that when the next (or 4th) generation of nuclear plant appears, it probably won’t make a great deal difference if it does take 5 or 6 years to construct a nuclear facility: in theory, 4th Generation equipment is greatly superior to previous models. I would also like to stress that I am familiar with many of the claims of nuclear failure that are in constant circulation throughout this old world of ours, but as it happens I am singularly unimpressed. American industry was able to bring about miracles during WW2 because for the most part pessimism and failure were not encouraged – as is NOT the case today with both nuclear energy and the U.S. macroeconomy. At the same time I am willing to admit that while many beliefs about the energy future that are often found in the U.S. and Sweden do not make any economic sense at all to me, I am convinced that if the citizens of those two countries continue to accept that more money is preferable to less money, then a different attitude toward nuclear energy will eventually appear. As David Schlageter pointed out in EnergyPulse (2008), “Renewable energy sources only supplement the electric grid with intermittent power that rarely matches the daily electrical demand.” He continues by saying that “In order for an electric system to remain stable, it needs large generators running 24/7 to create voltage stability. Wind and solar generation are not on-line when needed to meet energy demand, and therefore to help decrease system losses.” In the promised land of wind energy, Denmark, voltage stability is attained by drawing on the energy resources of Sweden and Germany (and perhaps Norway). The Danes pay for the imported electricity, but not for the stability – which they would do in the great world of neo-classical economic theory. It can be suggested though that the Danes may be unable to afford more than basics where electricity is concerned. According to NUS Consulting (of South Africa), the price of electricity in Denmark was the highest in the world in 2006 and the next highest in 2005. It can hardly be lower today. In 2005 Sweden had the next lowest price, and in 2006 the fourth lowest. Something must be drastically wrong in the Kingdom of Sweden for voters and politicians to remain passive in the face of this deterioration, particularly when NUS statistics indicate that the rise in the Swedish price is one of the most rapid in the world, and is almost certainly due to three things: a preposterous electric deregulation, membership in the European Union, and the closing of two nuclear reactors. The thing that should never be forgotten here is that for geographical and industrial reasons, Sweden is one of the most energy intensive countries in the world. As a result, a high energy consumption should be considered a necessity rather than a luxury. Before changing the subject, some information about the capacity factors of wind installations that was presented on EnergyPulse by Len Gould (2008) and Kenneth Kok (2008) can be cited. Unfortunately I cannot say whether these are extreme or typical cases, but they have one thing in common that all readers of this and other papers on energy economics should remember: the actual output from wind installations is often not just lower than the rated (or ‘nameplate’) output, but very much lower. Gould cites an operation by an independent North American wind power company in which the actual capacity factor for 2007 was somewhere between 8.67% and 17.35%. This might be characterized as a revolution in energy technology in reverse. Even so, it was superior to a performance noted by Kok, in which a TVA facility on Buffalo Mountain (near Oliver Springs, Tennessee) registered a capacity factor considerably under the above figures. In these circumstances it should be easy to understand why it was impossible to convince the voters and decision makers in Finland that in order to obtain the increase in electric energy that might be necessary for that country to maintain its standard of living, nuclear installations – with perhaps the highest capacity factors in the (base load) world – were preferable to windmills. For those readers who have been exposed to secondary school algebra, the above reference to things like voltage stability is superfluous. Over the last decade Sweden and Norway may have produced, on the average, the lowest cost electricity in the world. Norway, however, generates almost all its electricity with hydro, which is generally recognized as the lowest-cost power source, while Swedish electricity is produced in almost equal amounts by hydro and nuclear. On the basis of some elementary algebra presented later in this paper, it can be argued that the unit cost of Swedish nuclear power is equal to the unit cost of Norwegian (and Swedish) hydro. Strangely enough, this is an outcome that has not been welcomed by many observers in Sweden and Denmark, for whom the illusion of inexpensive and plentiful renewable energy is more real today than ever. Moreover this illusion is constantly reinforced by persons with a certain access to the media, but with only a minimum background in energy economics. But what about nuclear waste, which is repeatedly portrayed as a malicious and unavoidable cost of nuclear based electricity because, ostensibly, it will have to be locked up for hundreds of thousands of years? It is sometimes maintained however that the cost of disposing of nuclear waste is balanced by the benefit of no carbon-dioxide (CO2) emissions from reactors. For instance, the International Energy Agency (IEA) has calculated that for France – the country with the largest production of nuclear energy (as a per cent of the total output of electric power) – the average person is responsible for 6.3 tonnes of carbon dioxide (per year), which e.g. is one-third of the U.S. average. The cost-benefit trade-off mentioned above is worth remembering, however I prefer for students to know (and be able to explain) why France intends to treat ‘waste’ as a potential fuel. (A similar strategy has been proposed by the UK’s energy minister.) A law now exists in France stipulating that toxic waste is to be stored in such a way that it can be comparatively easily accessed and recycled if, at some point in the future, “new” technologies appear which will allow it to be classified a preferable input in the nuclear fuel cycle. The latter provision is, as the reader might guess, partially intended to appease or possibly bewilder nuclear sceptics, because technology is already available for recycling this ‘déchet’, and in the event that the price of newly mined and processed uranium escalates, it would almost certainly be utilized without further debate. A long exposition of how a recycling program might take place is found in a conference paper by Kenneth Kok (2007), and in a paper written with Ricardo Lopez (2008), Professor John Scire of the University of Nevada (Reno) proposes recycling as a substitute for storing the annual output of U.S. waste. Moreover, as pointed out by James Hopf (2008), nuclear plants in the U.S. are charged a fee of 0.1 cents/kWh to pay for the nuclear waste program, and just as important it is unlikely that this cost would ever exceed 0.25 cents. This is a comparatively small amount of money, which leads Hopf to suggest that where the management of “waste streams” is concerned, nuclear is a superior technology. The same conclusion is reached by Rhodes and Beller (2000)n, and here it needs to be emphasized that nuclear technology is in its infancy. The plant being constructed in Finland at Olkiluoto is a so called ‘third generation plant’, where the emphasis seems to be on eliminating the likelihood of a ‘meltdown’, but the real prize might turn out to be a ‘fourth generation’ installation, which operates at radically higher temperatures that permit a more thorough exploitation of its fuel. It has been suggested that this kind of facility will be especially important if the supply of uranium is reduced, however as noted by many comments published in EnergyPulse and elsewhere, few persons who work with or near uranium believe that there will be a shortage of this commodity in the foreseeable future, even if the forthcoming nuclear revival eventually assumed the dimensions of a Manhattan Project. It can also be mentioned en passant that there is at least as much fissionable thorium available in the crust of the earth as uranium, and Norway may well be a source of some of the largest deposits. Consequently, the bad consciences that some Norwegians seem to display because of the wealth of their country, will probably be shared by at least several future generations. In the case of Sweden, the low cost of nuclear and hydro power, and fairly smart regulation, made it possible to provide electricity to the industrial sector at a comparatively low price – at least until electric deregulation gained momentum. This being the case, nothing is more offbeat than hearing about the “subsidies” paid the nuclear sector. Cheap electricity meant the establishment of new enterprises, and just as important the expansion of existing firms. The tax revenue that was directly and indirectly generated by these activities, and used for things like health care and education, more than compensated taxpayers (in the aggregate) for any ‘subsidies’ that might have been dispensed by the government. An antithetical situation may prevail for wind and biofuels. In Germany the energy law guarantees operators of windmills and producers of solar energy an above-market price for power for as long as 20 years. This is an explicit subsidy, although it may be both economically and politically optimal due to the reduction in greenhouse gas emissions. More important, some inexpensive electricity for plug-in hybrids is made available. An especially complex subsidy apparently accompanies the exploitation of biofuels. Research taking place in the United States, and reported in the influential journal Science, claims that almost all biofuels used today result in more greenhouse gas emissions than conventional fuels if the pollution that is both directly and indirectly caused by producing these ‘green’ fuels is considered. In addition, there would be a substantial loss of ‘consumer surplus’ throughout the world due to a likely increase in food costs. Some of the intricacies of this important issue have been examined on an elementary level by Clay Ogg (2008). Against this background it might be argued that France’s total acceptance of nuclear power makes a great deal of sense, and its details deserve more attention. As noted in the Financial Times (October 6, 2006), nuclear power has provided “an abundance of cheaply-produced electricity, made the country a leader in nuclear technology worldwide and reduced its vulnerability to the fluctuations of the turbulent oil and gas markets.” France can also supply some electricity to neighbouring countries, which helps counterbalance the short sighted foolishness being promoted by the European Union’s Energy Directorate. (See also the survey by Murray Duffin (2004) and the comments on that survey.)
4. A MINIMAL OUTLINE OF THE NUCLEAR FUEL CYCLE “Satisfaction…came in a chain reaction.”
In my courses on energy economics and international finance, I have made a point of informing students that there are certain things that I expect them to learn perfectly if they prefer a passing to a failing grade, and the same will apply to the items in this section the next time I teach energy economics. The reason is simple, and is based on the likely appearance of considerable new nuclear capacity (especially in Russia, the U.S., India, China and Japan) that deserves to be studied and understood by persons who may find themselves in position to influence the configuration of the energy structure in their country or their local community, or for that matter merely to comprehend and explain some aspects of nuclear energy to friends and neighbours. There will also be new capacity in localities where politicians and their foot soldiers have repeatedly taken what amounts to a sacred vow to never think about or build or tolerate the construction of another reactor, because once TV audiences fully grasp what the lack of abundant energy will mean for them personally, an accelerated reassessment of the nuclear option will likely take place. It is often said that the world’s first ‘nuclear reactor’ – which in reality was an experimental device of a very primitive sort whose function was to obtain the first man-made sustained nuclear reaction – was constructed by Enrico Fermi. This took place in the squash courts under the stands of the football stadium at the University of Chicago. That charming stadium had been removed from the great world of (American) football because the University’s president regarded the sport as inconsistent with the intellectual grandeur he desired for the institution over which he had unfortunately been granted authority. The first peacetime nuclear plant was used to power the U.S. submarine Nautilus – although some observers preferred the label ‘wartime extension’ to ‘peacetime’. This was in January 1954. Six months later the Russians constructed a small nuclear-based installation whose purpose was to supply power to non-military users, and in October 1956 the first full-scale nuclear plant for civilian use was opened at Calder Hall in the UK. The first genuine ‘civilian’ power plant in the U.S. began operation in l958 at Shippingport, Pennsylvania. Perhaps the most interesting event during that phase of the Cold War however was the launching of the submarine USS Sea Wolf in l956, which evidently contained a liquid-sodium cooled breeder (or breeder-like) reactor of the type that Ralph Nader once referred to as “maniacal”. The ‘breeder’ will not be given much attention below, but it can be emphasized that its performance differs greatly from the light-water reactors (LWR) that form the major part of the U.S. nuclear inventory. Light-water reactors tend to feature two models: the boiling water reactor (BWR) and the pressurized water reactor (PWR). We can now turn to the simple physics of nuclear energy. Energy produced from fossil fuel is the result of an uncomplicated chemical process, however energy produced from nuclear fuel originates in the force binding the constituent parts of the fuel’s atoms together, and its release features the alteration of the structure of the atom itself. This is probably one of the reasons why the Nobel laureate Professor Dennis Gabor called the nuclear reactor the most important scientific achievement of all time. There may be some question as to whether it deserves that spectacular designation, but in many respects it is the most sophisticated. Two terms probably already found in the vocabularies of readers of this exposition are molecules and atoms, but they should be reminded that the latter is essential when examining the present topic. The expression molecule was coined by René Descartes in the 1620s, by which he meant an extremely minute particle: for the most part molecules cannot be seen with the naked eye, although apparently there are exceptions. Molecules are made up of at least two kinds of atoms in a definite arrangement, held together by strong chemical bonds. For instance, the water molecule is composed of hydrogen and oxygen atoms, and designated H2O. Atoms are generally thought of as ‘indivisible’, or the smallest particles characterizing a chemical element, but in reality sub-atomic particles have been identified. Almost all of an atom’s mass is found in its nucleus, which contains neutrons and (positively charged) protons, surrounded by swarms of (negatively charged) electrons, and the larger this nucleus, the easier it is to obtain the desired release of energy. Uranium is so important because one of the heaviest (and most complicated) atoms in nature is the isotope 235 of uranium, which is the only naturally occurring nuclear ‘fuel’ that will support a chain reaction. Its conventional designation is U-235, and it is important to know that different isotopes of an element occupy the same position in the periodic table, but they do not have the same weight. U-235 contains 235 ‘particles’, with 92 protons and 143 neutrons. The other isotope of uranium is U-238, with 92 protons and 146 neutrons. (The difference in weight is attributable to the neutron difference.) Fission is the breaking apart of a nucleus following the absorption of a neutron. If U-235 absorbs one additional neutron, it can become unstable and divide into two or more ‘fragments’ (sometimes called “atomic nuclei”), in addition to several neutrons. The mass of these fragments and neutrons is now somewhat less than that of the original nucleus and, most importantly, the reduction in mass corresponds to an increase in kinetic energy (i.e. motion), which is converted into heat as the fission products collide with surrounding atoms. Other U-235 atoms may absorb the neutrons released by a previous fission and themselves undergo fission. A release of neutrons that leads to further fission constitutes a “chain reaction”. What we have here is a mass-to-energy conversion of the kind associated with Albert Einstein’s famous equation E = mc2, where m is mass, c is the speed of light in a vacuum and E is energy. This equation specifies that the amount of energy that can potentially be released by only a small mass is huge. A complication however is that once a chain reaction develops, some sort of control is necessary to ensure that it continues at a steady level: sufficient but not an excess of neutrons must be obtained, and they must move at the right speed. On average this means that one neutron should lead to only one more fission. What is not desired is an uncontrolled exponential growth of fissions, which in the worst of cases could result in a meltdown, i.e. an overheating of the reactor core, or even an explosion. (It can also be noted that the neutron – discovered in l932 by James Chadwick – is the key to nuclear fission, because as a result of being neutral, it is not repelled by ‘Coulomb’ forces associated with atoms.) Occasionally we hear the expression critical mass in the discussion of this process. (This is also used in socio-dynamics, where it means the existence of sufficient momentum in a system so that the momentum becomes self-sustaining and fuels further growth. ‘Bandwagon effect’ was an expression that was popular when I studied economics, and it had to do with a kind of (social) critical mass.) It is important to appreciate that U-235 is fissile, but not U-238, however it is equally crucial to recognize that U-238 is fertile, which means that it can be the source of fissionable material not found in nature if it is bombarded with neutrons in a reactor. That material is plutonium (Pu, or Pu-239). Another fertile element is thorium, which was mentioned above, and reportedly is as abundant in nature as uranium. It can also be made fissile via neutron bombardment in a conventional reactor. Natural uranium consists of 99.3 percent U-238 and only 0.7 percent U-235, and any variant of uranium ore or processed uranium with the same isotopic composition found in nature carries the delineation ‘natural’. (There is a slight approximation here because there is a minute quantity (or ‘trace element’) of U-234 in natural uranium that is always ignored when discussing fission.) The relatively small amount of U-235 introduces a complication into obtaining a chain reaction, because enough enrichment must usually take place to raise the amount of U-235 in reactor fuel to at least 3%. At the same time it should be understood that there are reactors – such as the Canadian CANDU reactor – where unenriched natural uranium is an input. What characterizes this equipment is a thorough removal of non-uranium impurities, which together with the employment of suitably designed neutron reflectors and a heavy-water moderator can provide a chain reaction. Although enrichment is a very costly activity, there does not seem to be any hard evidence that (economically) CANDU type reactors are superior to light water equipment, apart from CANDU managers not having to worry about an unexpected spike in the cost of enrichment, which is a discomfort that LWR managers might suffer if enrichment takes place externally. The term ‘moderator’ used above has to do with reducing the speed of neutrons, so that the main source of energy is the break-up of heavy fissionable atoms that are struck by relatively slow rather than fast neutrons. Often the moderator is water or gas, but in the CANDU it is heavy water, which means water containing deuterium atoms. By way of contrast, the breeder is often called the ‘fast breeder’ because neutrons are not slowed down, and in the breeding process, neutrons from the splitting of Pu-239 convert non-fissile U-238 to additional Pu-239. According to Barre and Bauquis (2007), a unit of fuel in a breeder can provide almost 100 times more energy than it would in e.g. a LWR. Now for a brief resumé of the nuclear fuel cycle. The front end begins with mining. This activity is not as straightforward as it sounds, because the ore that is mined usually contains well under 1% uranium. In its pure form uranium is a silver-gray metallic chemical element that is approximately 70 percent more dense than lead (and weakly radioactive), and this metal can be obtained by crushing and grinding the ore. However, since there is relatively little demand for the metal, uranium is usually sold in the form of ‘yellowcake’, which is still classified as natural uranium. In A.D. Owen’s seminal book on the economics of uranium (1985), he states that one tonne (= 2204 pounds) of uranium metal (U) corresponds to 1.18 tonnes of yellowcake (U3O8). To obtain yellowcake, further processing in the form of milling and leaching (with sulphuric acid) must take place. In summation, the product of a uranium mine-mill complex is yellowcake, which on average is 70-90% uranium oxide (U3O8), and yellowcake is sold on a U3O8 content basis. The quoted price of ‘uranium’ that is presented in the trade literature is actually the price of yellowcake, which in turn is the price per pound of U3O8. Yellowcake is the basic raw material for fission fuel, and once obtained is converted into uranium hexafluoride (UF6), which is heated into a gas that is suitable for enrichment. As noted above, the purpose of enrichment is to increase the percentage of fissionable U-235 in a bundle of natural uranium from approximately 0.7 percent to about 3 percent, or perhaps slightly higher. The higher the degree of enrichment, the easier it is to maintain a chain reaction, and so the volume of the reactor can be reduced. (There has been a great deal of talk recently about certain countries taking enrichment to a point where they can obtain weapons-grade uranium, which means enrichment to about 93% U-235.) Uranium enrichment services are sold in Separative Work Units (SWUs), which is a measure of the amount of ‘effort’ needed to separate U-235 from U-238. A useful term in this process is depleted uranium (DU), or ‘tails’ , which is the byproduct of enrichment. It is the uranium remaining after removal of the enriched fraction. The tails also contains some U-235, but much less than that found in natural uranium. The remaining proportion is described in terms of a tails assay, and according to Owen (1985) is typically between 0.2 and 0.3 (as compared to 0.7 in natural uranium). The lower the tails assay, the more energy (in SWUs) required to produce a given amount of enriched uranium. It also turns out that producing a ton of enriched uranium requires about 6 tons of natural uranium, with the remaining 5 tons called depleted uranium (or tails). All enrichment is a very complicated (i.e. expensive) process, however its technology has been greatly advanced by moving from gaseous diffusion to the centrifuge system, and further improvements are almost certainly possible. Once UF6 is obtained, a further conversion into uranium dioxide (UO2) takes place, and this is fabricated into pellets. The pellets are loaded into specially designed tubes. In a light water reactor the rods are inserted into the reactor where fission takes place, and the ensuing heat raises steam in a boiler which turns a turbine-generator that produces electricity. From the boiler to the back end of the cycle a nuclear power plant is the same as a plant operating on coal or gas, with approximately the same thermodynamic characteristics. The thing to appreciate here is that a reactor is primarily a source of heat, and this heat is converted into mechanical energy by a turbine, and electricity via a generator. Much of this heat is lost, although clearly it could be a valuable input to households, industries and various commercial establishments. When a reactor has been in use for a certain period, the percentage of U-235 in it has decreased, and because of this and the contamination of the fuel elements by fission products, the efficiency of the chain reaction is reduced, and eventually it cannot be sustained. Spent fuel is then removed from the reactor and ‘fresh’ fuel inserted. The spent fuel is mostly (but not entirely) U-238 , and it cannot be used in ‘slow’ reactors, but if put in e.g. breeder reactors and exposed to high energy electrons, it can be converted to fissionable isotopes of plutonium. (This expression ‘tailings’ is also sometimes used with respect to spent fuel). A peculiarity with the cycle discussed above is that, theoretically, it is incomplete. The spent fuel that is taken from the reactor is usually stored, however instead it could be reprocessed and in one form or another fed back into the reactor, thereby completing the cycle. If this is not done, what we have is a once-through cycle, where the spent fuel is put into temporary storage, and kept there until consigned to permanent storage – preferably underground. Put another way however, this spent fuel is not ‘waste’ – which it is often called – but potential reactor fuel, because it contains an impressive amount of fissionable materials. Were it not for various political and environmental constraints, a larger amount of it would be turned into plutonium (which could be directly used in a breeder reactor) or a plutonium-laced mixture called MOX (mixed-oxide fuel) for reinsertion into modified conventional reactors. Perhaps the main bugaboo is that reprocessing involves the handling or availability of a relatively large amount of plutonium, which is a substance whose presence in large quantities is not to be recommended if our political masters deal with this commodity the same way that they often treat other potential menaces. By way of winding up this part of the exposition it should be noted that two terms that often appear when the conversation turns to reactors are thermal reactors and fast reactors. Both require a fissionable fuel, which for a fast reactor can mean Pu-239 as well as U-235, and both require a coolant to counteract the heat that is created as a result of fission. Thermal reactors also require a moderator to slow down neutrons, as well as various components to ensure that the fission is controllable. The fast reactor also requires a mechanism for control, but it is very different from that employed in a thermal reactor. These are a few other rather special items that could be taken note of, especially if the fast reactor is also a breeder (i.e. creates more fuel than it uses), but these cannot be discussed in an overview of this nature.
5. SOME BASIC ANALYTICS
Readers of this paper should now be in possession of sufficient terminology to convince fellow party animals that they have something useful to offer when the discussion turns from jazz or Frank Sinatra to nuclear energy; and for persons who feel at ease with the topic, the present section should enhance their knowledge of the subject. Particular attention should be paid to equation (2) below, even if the algebra before and after this relationship causes a problem. The items that will be taken up below are the capital cost of nuclear, followed by an output-input analysis that concludes with the so-called ‘burn-up’ (which has to do with the efficiency of using uranium), and finally, I want to discuss with a few equations a contention I have made in many lectures and informal conversations about the comparatively low cost of nuclear electricity. To be exact, since Sweden and Norway may still produce the lowest cost electricity in the world – although Norway employs almost exclusively hydro, and Sweden nuclear and hydro – some algebra shows that Swedish nuclear has about the same low cost as Norwegian and Swedish hydro. Although the lowest cost electricity does not mean that buyers of this good will always enjoy the lowest price, it is surprising (to me) to observe that over the past decade, the price of electricity in Sweden was among the lowest in the world. That price is rising now, largely because of Swedish entrance into the European Union. On the other hand, at the present time, Denmark has the highest electricity price in the industrial world, which can only be explained by its over-utilization of wind power. Next we can turn to a useful pedagogical first step for working our way toward a key economic concept. This involves a two year situation in which $1000 is borrowed and used to invest in an asset, for example, a mini-reactor that will be placed in the basement of your house, and which will be amortized in two payments over (an amortization period of) two years. The rate of interest (or the discount rate) in this example will be taken as 10% (or 0.10). (Amortization means repaying a debt, which in this example is tied to the purchase and cost of a reactor.) It is here that we introduce the term annuity, which is the amount (A) paid at the end of every period (e.g. year), and as will be calculated below, the annual amount ‘A’ is equal to $576. This means that in repaying the debt (=$1000), we pay $576 at the end of the first year, and also $576 at the end of the second year. The debt ‘today’ is $1000, and if paid at the end of two years, the lender would receive F = PV(1+r)T = 1000(1+0.1)2 =1210 dollars if 10% is the rate of interest. Let’s put this as follows: F in T years is equivalent to PV today. Also, please note that the $1000 is not the capital cost: it is the investment cost. We can take a closer look at this theme. There is a payment of $576 at the end of the first year, and this is equivalent to 576(1+0.1) = $633 at the end of the second year. If we add this to the annuity payment of $576 at the end of the second year, it sums to approximately $1210, or the same as above. It can thus be specified that, ceteris paribus, paying $1000 now for the asset, or paying $1210 at the end of two years, or paying $576 at the end of the first and second years are (in theory) equivalent, given that 10% is the applicable rate of interest.. Note the ceteris paribus criterion, because obviously in real life there are situations where this ‘equivalence’ would not be accepted, particularly by a lender. Something else that can be mentioned is that if the reactor had been paid for in cash removed from your wallet or purse at the time it was purchased, rather than borrowing to make the purchase, the concept of an annuity would still be valid. In this case the annuity payments represent the opportunity cost of purchasing this asset instead of e.g. lending the cash today and earning interest (amounting to e.g. $210 after two years). Now let’s generalize this two period example to T periods. Two equivalent arrangements for paying a debt of PV (called the present value) that is entered into at the beginning of the first period is to pay PV(1+r)T (= F) at the end of T periods, or via annuities ‘A’ at the end of each period (e.g. year), beginning with the end of the first period, and ending at the end of the last period! Thus we can write: PV (1+r)T = A + A(1+r) + A(1+r)2 +……..+ A(1+r)T-1 (1) This is a key expression, and if the reader has any problems here, he or she should work with the two period example given above. Next, multiplying both sides of this expression by (1+r) we obtain: (1+r)[PV(1+r)T] = A(1+r) + ………+ A(1+r)T We continue by subtracting the second of these expressions from the first: [(1+r)T] PV[1 – (1+r)] = A – A(1+r)T From this we obtain equation (2) below, which turns out to be:  If we make PV = 1000, r = 0.10 and T = 2, then we can calculate A = 576, as noted above. ‘A’ is generally referred to as ‘levelized cost’ in most of the technical literature relating to nuclear energy: it is the periodic payments for a reactor costing PV. This important expression could also be derived using elementary calculus, beginning with a fundamental (neo-classical) economics concept: the capital cost of an investment can be defined as the uniform return per period that an asset must earn, in order to achieve a net present value of zero. In other words, the asset price is the present value of future net yields (i.e. revenues minus costs). We can proceed by considering the output-input analysis of electricity production with a nuclear reactor, beginning with the observation that based on its atomic structure, 1 gram of pure U-235, completely fissioned, can produce 0.9 MWd (= 0.9 million watt-days = 0.9 megawatt days) of energy, and so the amount of U-235 necessary to produce 1 MWd of energy is 1.1 grams, assuming again that the fuel is completely fissioned in a perfect reactor – i.e. a reactor without heat loss. (An example is in order here. Suppose that you have an ideal reactor in your basement that is fuelled with 1.1 grams of pure U-235, and ten 100 watt bulbs (= 1000 watts) are burning all day every day in your humble abode. Then, if you could burn that uranium in some sort of ideal reactor-furnace, your house can shine brightly for 1000 (= 1,000,000/1000) days, where the units here are watt-days/watts = days. Note, 1 gram = 0.0022 pounds, which is a number that might be useful later on, as is 1 tonne = 2204 pounds.) But heat loss is a thermodynamic fact of life, and so to get 1 MWd(e) of electric energy we might need e.g. 3 MWd (thermal), where thermal relates to the fuel being used, which in this case is uranium. Accordingly, with one giga-watt (e) = 1 GE(e) = 1000 MW(e) operating over a year on the output side, our U-235 requirement on the input side is 3000 x 0.85 x 365 x 1.1 = 1,023,825 grams, where the assumption for this example is that the capacity factor – the fraction of a year that the reactor is actually operating – is 85%. Joseph Somsel though (2008) suggests that 90% is a more appropriate value. Note again the difference between MWd (energy) and MW (power), and MWd(e) and MWd(thermal). However heat loss is not the only bad news here, because the fuel that is inserted into a reactor is not pure U-235, as was indicated earlier in this paper. Instead it is a bundle of U-235 and U-238 that has been enriched from 0.7% of the former to at least 3%. As noted earlier, an item on the positive side is that some of the U-238 was converted by electron absorption to Pu-239 and fissioned, but this process is slower than the fissioning of U-235. It thus turns out that to complete our work we require a technological parameter that will tell us about the efficiency of utilization of the (enriched) uranium fuel – i.e. fuel containing both U-235 and U-238 – and this is called the burn-up. The burn-up is the total amount of heat energy created per unit of uranium fuel (i.e. enriched uranium)! In economics this would be called an input-output coefficient. A figure that I saw recently is 33,000 MWd per tonne (which corresponds to 33,000 x 1.1 grams (of U-235) per tonne of (enriched) uranium fuel), but the belief is that it can go higher. Put simply, the burn-up is the heat energy produced per unit of fuel weight. Using the previous calculation we get for the annual use of uranium by the reactor in order to generate 1000 MWd(e) the quotient [3000 x 0.85 x 365 / 33,000] = 28.2 tonnes of enriched uranium. (The input-output character of this calculation is best seen by forgetting about the uranium equivalencies that came into the picture with the use of the number 1.1, and simply noting that the MWd(thermal) input in order to obtain 1000 MWd(e) for a period of one year is 3000 x 0.85 x 365 MWd divided by 33000 MWd per tonne, and once again the answer (= 28.2) has for units tonnes (where l tonne = 1t = 2204 pounds). Remember that this 28.2 tonnes is enriched uranium, and so it might be possible to propose another input-output relationship between enriched and natural uranium. Using some numbers in the book of Professor Anthony Owen (1985) I calculated that 26 tonnes of enriched uranium corresponds to about 150 tonnes of natural uranium, and so the input-output coefficient is six. Thus, 28.2 tonnes of enriched uranium calls for 162 tonnes (t) of natural uranium. Next we use equation (2) to calculate the capital cost and the capital cost component of the energy cost for an interest rate of 5%, an investment cost (PV) of $2500 per kilowatt of capacity, and two values of T: 30 years and 60 years. ($2500 per kW of capacity is/was the investment cost for the US and EU used by the (French) General Directorate for Energy and Raw Materials, or (DGEMP), but once reactor construction achieves a faster pace, $1500/kW might be possible.) With T = 30 years, the levelized cost of a kilowatt of capacity is $162.5 dollars per year for 30 years, as calculated from equation (2). If we are interested in the energy cost (associated with that number) , and the capacity factor is e.g. 0.85, then we begin by noting that the amount of base load energy produced in a year by one kilowatt is 24 x 365 x 0.85 = 7446 kWh. The capital cost component of the energy cost is thus 162.5/7446 = $0.022/kWh = 2.2 cents/kWh. Now take T = 60. The levelized capacity (or capital) cost becomes $131.25/kW, while as a component of energy costs this is 131.25/7446 = $0.017/kWh. (The other components of the energy cost – the fuel cost and operations and maintenance (or O&M) cost – will be taken up in Section 6). Clearly, as T increases, the capital cost decreases. I chose 30 years to begin with because that is the value often seen when discussing the ‘life’ of nuclear facilities, but it happens that reactors are being constructed with an expected life of at least 60 or 70 years, and the lives of older reactors are being extended by upgrading. As for the interest rate used above, if the world functioned the way that I believe it should function, then the government would serve as a guarantor for amortization payments, and 5% would be a suitable interest rate to use in calculations of the type discussed above. As noted, the change in the capital cost that resulted from increasing T from 30 to 60 was comparatively small, however specialists in this topic are more concerned with the situation after T, when the capital cost is amortized, and buyers of electricity have access to electricity whose cost is only due to the cost of fuel and O&M. The same of course is true for electricity generated using gas and coal, however relatively speaking a large increase in the price of gas and coal has a much greater effect on the price of electricity than a corresponding increase in the price of uranium (i.e. yellowcake). With regard to the above calculation, I have absolutely no influence over the interest rate at which money can be borrowed by firms producing nuclear-based electricity, and so 5% is probably too low to use as a discount factor in the calculations made above. This matter will be taken up again Section 6 below, and another calculation will be made using more realistic figures. I can mention however that the numbers obtained later for the capital component of the energy cost are fairly close to those obtained by the French Commissariat de Plan, and reproduced by Barre and Bauquis (2007). The last exercise in this section involves a statement about the relative cost of nuclear, where relative means that it will be compared to hydro – which is the most inexpensive generator of electricity. Moreover, according to easily available data, the (average production) cost of electricity in Sweden, which involves hydro (H) and nuclear (N) is about the same as the average cost of hydro generated electricity in Norway. (The price to consumers may or may not be the same, which is irrelevant for the present discussion). Calling Sweden country 1, and Norway country 2, the following algebra seems appropriate, where C/q (Cost/quantity) represents average cost: 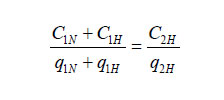
This can be written in the following manner, where q is the total output of electricity in Sweden: Both sides of this expression can now be multiplied by q, and in addition q1N can be taken as ?q and q1H as (1 – ?)q. Using these in the above expression we are then able to write the above expression as 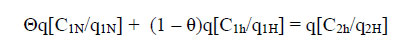 The q’s can be cancelled, and making the reasonable assumption that C1H/q1H = C2H/q2H, some simple manipulations will give us: 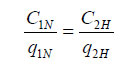 What this says is that the average cost of nuclear generated electricity in Sweden is equal to the average cost of hydro generated electricity in Norway, which in turn is probably the lowest cost electricity in the world. The price of uranium (fuel) is a topic that requires an extensive discussion, but while that discussion is comparatively simple, it will have to be provided elsewhere. It can be mentioned though that even if the price of yellowcake greatly increases, students of this topic have expressed no alarm. They know that if (or when) uranium (and thorium) become scarce, there will be more reprocessing of spent fuel, and in addition – for better or worse – the breeder reactor will have its opportunity. Some of us however are not enthusiastic about the latter option. 6. SOME ECONOMICS OF LOAD DIVISION
We can begin this section by specifying three kinds of equipment that can produce electricity. These are gas-based, with a low capital cost (F1), but a high variable cost (v1); coal, with a capital cost (F2) that is higher than gas, but a variable cost (v2) that is lower; and finally nuclear with the highest capital cost (F3), but the lowest variable cost (v3). This arrangement can be seen in the top diagram of Figure 2a. Once again the cost relationships are linear and of the type C = F + vt, with the applicable part of these curves being the solid lines that form the aggregate cost curve, The discussion usually involves a capacity of 1 kW, but these screening (i.e. cost) curves are applicable for any capacity. 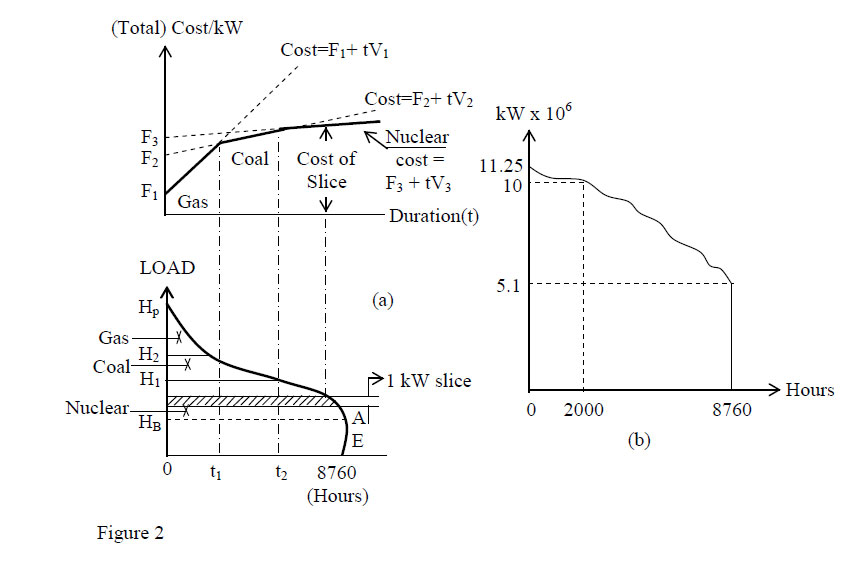 In turning to Figure 2, we can begin with 2b, which shows the load on the line in Norway in 1975. The maximum load was 11.25 x 106 kW, while during 2000 hours of the year the load varied between 11.25 x 106 and10 x 106 kW. Between 2000 hours and one year (= 8760 hours), the load was between 11.25 x 106 and 5.1 x 106 kW. As can be noticed, never during the year did it fall below 5.1 x 106 kW, and so it is clearly appropriate to designate 5.1 x 106 kW as the base load, although it could happen that the base load equipment supplies some of the intermediate load. What about the intermediate and peak load? This is more or less subjective, however I am sure that Norwegian engineers were capable of making the optimal choice, whatever it turned out to be. The exposition will continue by extending the examples given in the previous section. The first step is to put the load diagram at the bottom of Figure 2a into perspective with the screening (i.e. cost) curves at the top of Figure 2a. As in the previous section we can write as the values of the costs C1 = F1 + v1t, C2 = F2 + v2t and C3 = F3 + v3t. Something that can be noted again is the expression merit order, where the intention is to determine which type of equipment carries which load, and over what portion of the year (of 8760 hours). What we are going to find out with some simple algebra is that in the arrangement in the figure, gas generates the peak load, coal generates a part of the intermediate load, and nuclear generates the remainder, which in this diagram means the base load plus a part of the intermediate load. Accordingly, during a part of the time nuclear is idle, and so it might be designated a reserve, since after all there is considerable uncertainty associated with the ex-ante (i.e. before-the-fact or predicted) load. It might be argued that this is a bad example, since it is a waste to have expensive nuclear equipment idle, however given the cost curves, the specification of cost-minimization leaves us with no choice. (It seems that a reserve of 15-20% is usually deemed correct, although at the present time in the U.S. and perhaps other countries it has been suggested that there has been serious underinvestment in power sources and especially transmission lines.) Using the algebra and elementary logic from the previous section, it is a simple matter to find t1 and t2 in the above diagram. To get t1 we start with F1 + v1t = F2 + v2t. This immediately gives us F2 – F1 = t (v1 – v2), and so t = t1 = (F2 – F1)/(v1 – v2)). Obtaining t2 is just as easy, but it will be left for you to do as an exercise. Notice also that from the point of view of signs, the value of t1 makes sense, because F2 > F1 and v1 > v2, and thus the quotient is positive. Let’s also notice that in this example if we say that we have a peak, intermediate, and base load, only the base load 0-HB is unambiguous. The peak load definitely appears to be H2-HP and the intermediate load HB-H2, but aside from the algebra there is a certain ambiguity about these two which is not important for the readers of this book – nor for its author. We can imagine a number of hypothetical situations which would have a place in this discussion. For instance, one might be that after we make our calculations, gas carries none of the load. Why? The only possible answer is that it costs too much relative to coal and nuclear. On the other hand, it may carry the entire load. Why? The short answer is that it is less expensive than the other options. Consider the situation in California over the past decade. As a result of technology improving combined cycle gas-based equipment until it became very efficient, and the gas price remaining very low until the last few years, gas based equipment became sufficiently economical to generate a much larger share of the electric load in that state than previously contemplated. The same thing happened in the UK with the so called ‘dash for gas’. As bad luck would have it though, the gas price suddenly escalated, and while existing gas-based equipment could not be instantaneously discarded, when new generating equipment was considered, gas looked much less attractive. Accordingly there is a difference between the optimal merit order and the existing merit order. Readers who have come this far without feeling frustrated can feel very satisfied, because in truth I am always amazed by the shortage of knowledge about nuclear economics. It’s interesting to note that in Australia, plants that are designated intermediate load plants comprise about 40-45 percent of total installed capacity, as compared to 50 percent for base load plants, and 5-10 percent for peaking plants. This says something about the place of uncertainty in these matters and how it causes a deviation from the ‘ideal’ or optimal merit order of the type being presented above where we get unambiguous answers as to the value of t1 and t2. Generally the peak load represents only a small fraction of the demand for electricity, and it can happen that only a portion of this capacity is in use, but since the available generating equipment must be able to satisfy the maximum demand that may appear in the system, capacity or load factors for peak load facilities are often quite small. As a result, if possible, as much peak load power as possible should be purchased rather than generated in the system, and as a result many utilities do everything possible to satisfy these requirements by purchases from other cities, states, regions or countries. The expression load factors was used above. This can be defined as the Average Load divided by the Peak Load. Ideally this is fairly large (i.e. close to unity), but there can be some ugly surprises where electric generation is concerned, and so in some regions considerable excess or reserve capacity must be available because there can be a simultaneous peak in neighbouring regions. In some classroom discussions students want a formalization of the results presented above on ‘load division’. Here I can point to an important article by Michael Einhorn (1983) whose mathematics I have altered somewhat to correspond to my classroom presentations of this topic. The following expression should be self-evident if the reader comprehends Figure2, and is familiar with integral calculus. 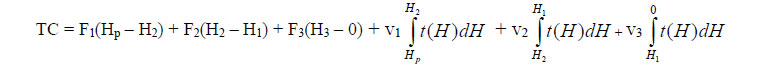 Integrations take place horizontally, and involve slices of the capacity H bounded by the vertical axis and the systems load curve. This is synonymous to equation (4): 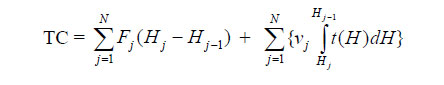 Next we differentiate TC with respect to, for example Hj, and set the resulting expression equal to zero. This gives us (5): 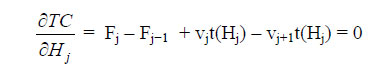 From this we obtain for a cross-over time: 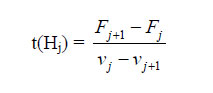 For instance: 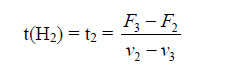 We have an overtone of (Albert) Einstein’s equivalence theorem here in that two approaches (informal and formal) lead us to the same result, which suggests that the same fundamental law is operating, and the informal presentation was also about cost minimization.
7. MORE BACKGROUND FOR CURIOUS READERS
One of the most brilliant appendages to the topic that we are discussing can be found in a non-technical article by the late Samuel Schurr (1988). Concentrating on the United States, Schurr demonstrated that the total energy use in what he termed the “business sector” more than doubled over the period 1920-73, and in relation to capital ( = machinery + structures) increased by 50%. The observed slight fall in the energy intensity of output was then shown to be due to technical change (largely motivated by increasingly energy intensive inputs) raising output by so much that, percentage-wise, output increased by more than the increase in energy consumption. (It was due to the failure to understand the details of this phenomenon that many concerned observers found themselves confronting and often elaborating on the bogus argument that output could be maintained or for that matter increased even if the input of energy declined.) Schurr also hypothesized that electrification meant a flexibility in industrial operations that would have been impossible with any other form of energy, and this was the cardinal reason for productivity growth. Equally as important, electricity would play an indispensable role in the employment of items such as computers, whose revolutionary promise was just being realized. If this is the actual situation, then an intelligent economist living in complete isolation from the ‘real world’ – which, unfortunately, is a world in which security problems cannot be ignored – might suggest that the best strategy for fostering economic growth, as well as stabilizing or reducing atmospheric greenhouse gases, is a massive program of nuclear construction, and it should be commenced as soon as possible. This humble commentator is definitely in favour of more nuclear, but at the same time it seems appropriate to wait until security problems assume another dimension before anything resembling a “massive” commitment is undertaken. In addition, it needs to be emphasized that an optimal energy ‘package’ for any region probably contains a very large component of renewables. A country that illustrates to some extent the last observation is of course China. In 2007, 3.4 gigawatts (= 3.4 GW = 3.4 billion watts) of wind-based capacity was added to China’s electric grid, while by 2020 the desire is to raise nuclear capacity from its present 10 GW to 40 GW, which is the fastest proposed increase in the world. Similarly, the intention is to add 1300 GW to China’s total electric generating capacity by 2020 (which can be compared with the total present U.S. capacity of 1000 GW). Unfortunately, however, regardless of the amount of nuclear, wind and solar that the Chinese deploy, a large amount of coal will almost certainly be consumed. A question that should therefore be asked the anti-nuclear booster club is would they like the government of China to cancel its nuclear and hydro programs, because this would result in an even greater increase in the output of carbon dioxide generated in that country. The problems brought about by coal have been touched on briefly in my textbooks and also my book on coal (1985), but this is an issue that requires additional consideration, because despite increased concern over global warming, it is very unlikely that the growing world population will ignore the energy in that commodity. An important discussion of coal in Europe that applies to other regions can be found in a short paper by Jeffrey H. Michel (2008), and in a personal communication Michel informed me that Carbon Capture and Storage (CCS) would be extremely energy consuming “and consume twice the water of conventional power generation, making its wide-scale implementation doubtful.” Although it cannot be taken up here, the Swedish utility Vattenfall used the increased profits made possible by electric deregulation in Sweden and open borders in Europe to raise electricity prices in Sweden, and also to expand their coal producing operations in Germany. Despite assurances to the contrary, this latter commitment will not have anything to do with reducing CO2, since with the blessing of the Swedish government – which has access to a nice slice of its profits – Vattenfall intends to focus on increasing activities outside Sweden.. Observing the Swedish nuclear past provides a valuable but generally unappreciated insight into mechanics and digressions of what Professor Ken-Ichi Matsui (l998) calls the “Seventh Energy Revolution”, which he believes will be based on nuclear energy. This is so because in Sweden natural gas has often been singled out as one of the main replacements for nuclear. As alluded to earlier, the main advantage of nuclear as compared to gas based equipment was in the cost of the fuel, which meant that gas was at a disadvantage for carrying the base load, although the capital cost of a nuclear facility was much greater. When, however, combined cycle gas-burning equipment became widely available, and in addition the price of gas fell, it was claimed by persons who should have known better that gas would always be much more economical than nuclear (for generating the base as well as peak loads). With the price of gas in the vicinity of 3.5 dollars per million Btu ( = $3.5/mBtu), it was easy to insist that gas was a better economic bet than nuclear, and a locale where this was argued at great length was California.. In Sweden, if an accurate (and comprehensive) calculation had been made, if notice had been taken of what was taking place in the rest of the world, and especially if there was less technofobia in and around the political establishment, the claims made about gas would have been openly ridiculed, because it has long been obvious to many of us that the infinite supply of gas that a number of so-called energy experts were thinking of was actually finite – as everybody is either finding out now or will soon find out; and since environmental considerations dealing with CO2 were becoming more important, nuclear displays am indisputable social cost advantage over gas. Here I can mention that a few years ago, when the cost of gas first touched $7/MBtu (= $7 per million British Thermal Units), many reputable sources claimed that it would reach $10/MBtu by 2012. In point of truth, the price of gas could reach that level before the present year (2008) is out, and since there will still be a large gap between the BTU price of oil and gas, the price of gas will almost certainly continue to rise. Readers who want an up-to-date examination of the prices of energy resources should turn to the site ‘321 Energy’, which can be reached via GOOGLE. They will also find on that site a large collection of non-technical articles published in the international press. Another example might be useful here. The first time that I taught in Australia it was widely advertised that the Maui gas field in New Zealand was virtually inexhaustible. The reserve situation is quite different at the present time, however that field is still spoken of as being extremely valuable. Not, it should be emphasized, for producing natural gas, but for storing – or ‘sequestering’ as they say – as much as possible of the CO2 that will be generated in the coal-based generating facilities that will eventually be required in this century to provide New Zealand with an increasing fraction of its electricity. It can also be mentioned that the New Zealand electricity deregulation, which at one time was praised as the most satisfactory in the world, was very likely based on beliefs about the availability of gas that were completely illusory. I suspect that this was an important factor in establishing a natural gas price for that country that was probably lower than what in economic theory is sometimes termed the ‘scarcity price’ (or the theoretically correct market price). According to Torsten Gustafson, chief scientific advisor to the Social Democratic government of Tage Erlander, there was a positive attitude toward nuclear energy in Sweden until about 1970. After that time, two of the five major political parties in Sweden – the ‘farmer party’ and the communists – came to the grotesque conclusion that the ‘friendly atom’ was bad for Sweden and just about everyone else, although there were a number of opponents to nuclear energy in all political and social factions. There is no rational explanation for the strong aversion developed by any political grouping to nuclear energy, since e.g. farmers and industrial workers were clearly important benefactors of inexpensive electricity. This situation could probably be compared to something like the ‘tulip bubble’ in Holland in the 17th century, when intelligent people suddenly and inexplicably discerned enormously valuable qualities in the humble tulip, and paid fantastic prices for a commodity that eventually turned out to have no commercial and little intrinsic worth. The commodity in the present case is the belief in nuclear disengagement, which might provide a modest slice of the voting public with a tangible psychological satisfaction in the short run, but in the long run would deprive Swedish industries and households of the comparatively low-priced access to an indispensable input. The final topic in this section is the almost unknown concept of the so-called ‘backstop technology’, which as outlined by William Nordhaus in a brilliant article (1973) is the technology used to exploit a resource or asset that will still be available when all or most of the conventional resources are history. Not much is heard of the backstop these days, and I doubt whether I mentioned it in my energy economics textbooks, but there was a time when – in my lectures – I always brought it up in the context of discussing nuclear energy, although unlike Professor Nordhaus I treated it as a means for supplying the ‘extra energy’ needed to produce motor fuel or energy liquids from biological resources. For instance, although not widely known, Sweden possesses large quantities of low-grade uranium, and eventually science and technology will make it feasible to utilize these resources in a politically and environmentally approved manner. As a result, they might make an impressive contribution to the Swedish economy. For the purposes of this exposition, a backstop is a known technology for producing a very large amount of a given resource at a known price. (Actually, Nordhaus thought in terms of an infinite amount.) Suppose for instance that at a certain time only coal was used to produce electricity, but there is only a limited amount of coal in the crust of the earth. When, however, this coal is exhausted, we will still desire electricity over a very large number of years in the future, and so it is necessary to think about an alternative technology for producing electricity that is more than a ‘stopgap’. One candidate might be uranium and thorium burned in breeder reactors, because given the likely amounts of these resources, they would be capable of producing electricity for many decades, or even centuries. Please be assured though that this statement is NOT an advertisement for the breeder. A different example that might be applicable is oil from coal functioning as a backstop for conventional crude oil. As is well known, there are technologies available that can provide large amounts of liquids that can fulfil the present functions of crude oil. (Observe that I said large but not, as Nordhaus, an infinite amount.) A trivial example will now be formulated for the purpose of obtaining a not very profound result, but one that needs to be spelled out in the light of what is happening at present on the oil market. Suppose that crude oil is finite in supply, with B units available until the global supply peaks (i.e. begins to decline), and this oil can be extracted at zero (marginal and average) cost. Moreover, every year A units are extracted. This means that, ceteris paribus, it will be possible to extract oil for T = B/A years until its output inexorably begins to fall. Thus, at the end of T years, if we want to continue enjoying A units of oil, or an oil equivalent, we must have a supplementary technology available that will allow us to produce the difference between A and the global output whatever that turns out to be. To keep things simple, suppose that this ‘peaking’ amounts to a sudden decline in output to Q, at which level it is believed that it will be maintained, and we define X = A – Q(T). Suppose also that the technology that will allow us to produce X units of oil indefinitely will cost Z dollars. Its cost today, at time ‘t’, is thus Ze-r(T-t), where r is a discount rate. In other words, if we put this amount in a bank, and the interest rate was ‘r’. then in (T – t) years it would grow to Z, and we would be able to purchase this technology. The next step is elementary. If the technology costs Z, and we desire A units, then the cost of obtaining one unit of this oil is Z/[A – Q(T)] = Z/X = F, or what is the same F(T). Since we said that at present oil can be extracted at zero cost, if it were not for the exhaustibility of the resource the present price would be zero, but instead we must remember the need to purchase a new technology in T years, and so the (theoretical) oil price at the present time is p(t) = F(T)e-r(T-t). In a perfect (or textbook) world the market would provide this price. When I began teaching energy economics, T (for oil) was far, far away. Now there are people who believe that it is no more than a few years in the future. In a textbook world we would know exactly when T would arrive, and take steps to ensure that we had the oil needed to ensure that every winter we could make our way to the skiing and partying in the north of Sweden. For instance, in terms of the discussion above that involves Sweden, it might mean having reactors that could supply the extra energy needed to produce e.g. synthetic oil. A little calculus will show that if more oil was found, the time when synthetic oil would be required would be pushed further into the future, and so p(t) would be smaller. It is also possible at the cost of some complication to solve this problem for an arrangement where the decline in Q after T years is not in the form of a ‘step function’, but instead takes on the form of the ‘tail’ of a normal distribution. I prefer to leave these extensions to someone else, while stressing that in a world in which the peak oil hypothesis is gaining increasing support, an increase in the price of oil and the increasing respectability of nuclear energy makes all the economic sense in the world.
8. FURTHER ASPECTS OF NUCLEAR COSTS
One of the assumptions in my new textbook is that even if natural gas were available at bargain-basement prices (which is no longer likely), it would be sub-optimal to unconditionally regard it as preferable to nuclear where new energy investments are concerned. The thing to be aware of here is that the global output of gas might peak in twenty or thirty years, while a new nuclear installation will be on line for at least 60 years, and could still have access to comparatively inexpensive fuel. The peaking of gas during the lifetime of nuclear installations constructed e.g. today will increase the opportunity cost of that resource in such a way as to make it extremely difficult to comprehend why, in Sweden, it has become possible to consider gas a replacement for nuclear. Remember too that there is a fairly high environmental cost associated with natural gas, though not as high as coal. An important though straightforward discussion of the cost of energy resources can be found in Chapter 8 of Barre and Bauquis (2008). What I will do now is to recalculate the capital component of the energy cost using the same technique as in Section 4 above. Then I will ‘scale’ the values of the fuel and O&M components of the energy cost from the work presented in that chapter. It turns out that this will provide me with a value for the energy cost of a kilowatt hour of electricity close to that suggested by Jim Beyer (2008), who is one of the many important contributors to EnergyPulse. (Beyer’s comment is surrounded by other remarks about the cost of nuclear energy.) What will be done first is to make a calculation based on what I consider representative values for I, T, and r. These are I = 2600 dollars, T = 40 years, and r = 10%. I continue to use a capacity factor of 0.85, although possibly this is too low, Using equation (2) in Section 4, I get a levelized capital cost of $265 dollars per kilowatt, which in turn gives for the capital component of the total cost 3.5 cents per kilowatt hour. Then, using the values for capital, fuel and O&M costs in Chapter 8 of Barre and Bauquis as a datum, I get 2.61 cents/kWh for the fuel component of the energy cost, and 1.40 cents/kWh for the O&M component of the energy cost. The total energy cost is the sum of these, or 7.5 cents/kWh, which comes sufficiently close to Bayer’s value of 8 cents/kWh for the U.S., and James Hopf’s 6.8-8.2 cents/kWh (2008) to make it useful for this exposition. The Economist (July 9, 2005) has presented some estimates from several sources for average electricity costs. For German utilities the Union Bank of Switzerland (UBS) gives 1.5 cents/kwh for nuclear, 3.1-3.8 cents/kWh for gas, and 3.8-4.4 cents/kWh for coal. Similarly, they give 1.7 cents/kwh for nuclear in the US, 2 cents/kWh for coal, and 5.7 cents/kWh for gas. James Hopf (2008) has identified these as fuel costs, and in the same ‘string’ of comments he provides important information on O&M costs for nuclear. The (IEA), employing a discount rate of 5%, argues that energy costs for nuclear are $21-31/Mwh, while gas ranges from $37-60/Mwh In a summary of generating costs originating with the International Energy Agency (IEA) and OECD, Tarjei Kristiansen of Statkraft Energi AS (Norway), claimed that with a 5% discount rate, energy costs in $/MWh are 23-31 for nuclear, 25-50 for coal, and 37-60 for natural gas. The only comment that I have on these results is that – on the average – they might be accurate for some countries and inaccurate for others, but for me the best discussion of this issue is found in the comments on my 2008 article in EnergyPulse. In addition, in the calculations in Section 4 above, I used a burnup of 33,000, but I recall Professor Ulf Hansen of Rostock University remarking at a conference that the average burnup now might be between 45,000 and 50,000. If this is true, and at the same time all countries could construct nuclear facilities in 4 years – which the Japanese have shown to be possible – and the life of a new nuclear installation is at least 70 years, which I regard as certain, then a more careful analysis than that carried out in this paper should reveal that nuclear energy is a very competitive medium for carrying the electricity base load. But what about coal and wind, which appear in Barre and Bauquis as important competitors to nuclear, though the figures these authors present indicate that they are unequivocally more costly. A large part of the explanation for their inferiority turns on the very high carbon dioxide (emissions) cost associated with coal, and the lack of reliability of wind. (This lack of reliability can also be expressed as a cost). The same applies to solar, though perhaps less than wind unless we are talking about places like northern Europe. In considering relative or intertemporal costs it is necessary to have some idea of the resource base. According to estimates of the World Nuclear Association in 2000, the country with the largest uranium reserves is Australia, whose reserves at that time were 622,000 metric tons ( = 622,000 tonnes = 622,000t), and whose production was 7,720t. In what follows I would denote this as (622,000; 7,720). This discrepancy seems very large, but not when I remember the negative attitudes toward the production of uranium by my mathematical economics students in Sydney and Melbourne. The largest producer was Canada, with a production of 12,520t and reserves of 331,000t = (331,000; 12,520). Other important countries were Kazakhstan (439,200; 2018), Namibia (156,120; 2,239), Niger (69,960; 3,095), Russia (145,000; 2,000), United States (110,000; 1000), Uzbekistan (66,210; 2,400), other (306, 940; 2774). Total estimated reserves in 2000 were thus 2,246,430t, while production was 35,767 tonnes. For technical details see Owen (1985), but the total input of uranium in e.g. the production of electricity exceeds 35,767 tonnes because a great deal of the resource can be obtained from the recycling of spent fuel and former military ordnance. Sweden does not appear above because exploiting its low-grade reserves is uneconomical at the present time. Eventually this situation could change because of scientific and technological improvements in mining and processing. Something that might cause a quantum jump in the value of Swedish uranium however would be the breeder reactor becoming a commercial proposition, because in that case the output of energy (due to the exploitation of the plutonium that could be bred) would make it economical to use even low-grade uranium. As far as I am concerned though, the Swedish government (and most other governments) are at present completely incapable of solving the security problems that would be posed by a greater presence of and/or reliance on plutonium. This may be the only point on which I happen to be in agreement with people like Ralph Nader and Amory Lovins. Unlike them, however, I happen to believe that by rejecting the energy in uranium when it is used in ‘conventional’ reactors, the (psychological) conditions are being created for a panic-stricken rush into the breeder when the fundamental scarcity of oil and gas – and the present inadequacy of renewables – is made clear to the television audience. An interesting factor here is that Sweden was at one time believed to be surrounded by comparatively unsafe reactors: a total of six were said to be found at Sosnowy Bor outside St Petersburg (Russia), and Ignalina in Lithuania. In the film The Deer Hunter, Christopher Walken sang a drunken version of the marvelous tune ‘I’ve got my eyes on you’, and many nuclear experts in Sweden have had their eyes on Ignalina as an installation (of the Chernobyl type) that could pose a danger to this country, but not the ‘Greens’. Their eyes instead have been fixed on safe reactors in Sweden, as well as the new super-safe facility that is now under construction in Finland, and which will have a rated output of 1600 megawatts, or as much as the two Swedish reactors that were closed at Barsebäck (near Malmö). Somebody else with a keen interest in reactors is Mr Romano Prodi of the EU, who is one of the overseers of the ridiculous crusade to deregulate Europe’s electricity and gas. Among the reactors in which he has taken a particular interest are those of Bulgaria, which the International Atomic Energy Agency (IAEA) considers to be on a par with the average in Western Europe. According to John Ritch, the US ambassador to the IAEA, the European Commission has decided to “blackmail” Bulgaria in such a way as to make its entry into the EU contingent on its willingness to reduce its nuclear capacity. Even a combination of John Maynard Keynes and Sigmund Freud would have a difficult time comprehending the reasoning here, although Mr Ritch feels that this scheme originates with the “antinuclear environmentalists” that play an important role in the Prodi team. This may be true, but as I pointed out in a talk in Milan several years ago, it may also have to do with a belief by the Prodi braintrust that since half of Bulgaria’s electricity came from nuclear reactors (as compared to 30% in Europe overall), electricity deregulation in that corner of Europe would be easier if Bulgaria’s nuclear capability was reduced. Theoretically this makes sense, because in Sweden competition – which was supposed to be the object of deregulation – decreased rather than increased after deregulation was introduced: e.g. large generators have been able to merge with smaller firms. Ideally, this paper would include a discussion of the optimal plant mix, and O&M costs would have been handled in a more sophisticated way than scaling the results of other authors. Where the first is concerned I refer to my textbooks, and as for the second the scope and complexity of O&M costs are mostly unknown to myself, however the bottom layer of comments on my 2008 article in EnergyPulse (www.EnergyPulse.net) should illuminate a large part of this subject. Something was said above however about the amount of fuel required to obtain a certain annual energy output, and given the price of e.g. yellowcake (which is listed daily in ‘321 Energy’) obtaining the cost of an annual reactor load should hardly be a challenge to interested persons. A problem here though is that the price of reactor fuel can be expected to increase. One way to think about this is to assume that it increases at a steady rate (e.g. ‘g’ percent per year), and calculate its present value (PV) using an appropriate discount factor (r). Once we have that we can obtain the value of an annuity from equation (2). In the real world decision makers might not be interested in this approach, but it looks nice in a seminar or a class room. The mathematics here is straightforward. If we have a cost ‘z’ at time ‘0’, and it increases at a rate ‘g’ over the time horizon T, then for time ‘t’ we can write zt = z0egt. This can be discounted back to time t(0) to obtain a present value PV, or PV(zt) = z0egte-rt = z0e-(r-g)t, and it simplifies the algebra if we have r > g. The next step is to sum the PVs over some time horizon T, and so with continuous discounting we can write: Expression (5) can be turned into an annual charge by using the continuous version of the annuity formula, which is given at the top of the paragraph beneath equation (3). In this case it can be written as A = rerT/erT – 1, which for this discussion in more convenient in the form A = r/(1 – e-rT). We can now complete the derivation by writing;  Although not immediately apparent, this result matches the one obtained by Professor George Yarrow of Oxford University (1988) in an important article.
9. NUCLEAR AND THE KYOTO HOBBY-HORSE
As I have found out, it would not be a good idea in Sweden (and probably elsewhere) to belittle the Kyoto Protocol if you are anxious to impress the Broad Masses with your wisdom – or at least that portion of them with the typically “deep interest” in environmental matters that characterizes many of the ladies and gentlemen heavily involved in economic research in Sweden. The basic problem here is that this sub-set of the BM doesn’t really understand the issue. They don’t understand that at bottom the Kyoto Conference itself had little or nothing to do with reducing Greenhouse gases, and might best be described as an outstanding example of what George Orwell called a system of indoor welfare. Michael Hanlon, the science editor of the Daily Mail (UK) puts it as follows:
Among the “people” that Mr Hanlon is describing were most of the ‘delegates’ to Kyoto, whose principal interest was to obtain tickets for the next climate warming jamboree. According to Professor Sven Kullander and several colleagues in the Swedish Academy of Science (2002), Kyoto was an important first step for reducing greenhouse gases, but “helt otillräckligt för en reell förbättring” (= completely insufficient for a real improvement). If readers can accept the latter portion of this judgement, then I accept the first part – although in reality I put the Kyoto meeting in the same category as the ‘World Summit’ in Capetown, where perhaps 60,000 heavy eaters and drinkers assembled to solve in their own gluttonous way the many and varied problems confronting contemporary societies. Swedes accept Kyoto for the same reason that they accept electricity deregulation and the EU: they were told to accept it by celebrity politicians and journalists. The physicist Richard Feynman once said that in matters of the above nature the logic of science is superior to that of the authorities, but a hypothesis of that nature has no place in the pretentious deliberations of assorted media favourites, which assures that it is taboo for a large part of their audiences – at least when they are sober. Swedes are also great partisans of ‘emissions trading’, although an advisor to President Putin once called it a scheme to make money that is irrelevant for suppressing greenhouse gases. I also have published a number of similar comments on this topic, in addition to providing many for persons attending my lectures, but I am afraid that the latter would be out of place here.
10. ITALY JOINS THE NUCLEAR THAW
In l987 – following the Chernobyl nuclear disaster – Italy voted to abandon nuclear, and a similar gesture was made by the good people of Sweden about the same time. According to the (UK) Financial Times (February 24, 2009), Italy’s “relatively advanced nuclear capacity was (immediately) mothballed or dismantled.” Fortunately though, Sweden specified 2010 as the date for dismantlement, because over the last decade Swedish nuclear energy – together with hydro – has provided this country (Sweden) with perhaps the lowest cost electricity in the world, and until the curse of electric deregulation appeared, the price was also among the lowest in the world. The new Italian facilities are scheduled to be constructed by ENEL, with the cooperation of Electricité de France (EDF), who played a key role in the design of the reactors to be installed. This equipment will not make its appearance in Italy in the very near future though, and in fact if there is a serious nuclear accident near that country, it may never come into existence. But given the nuclear renaissance that is gaining momentum in Europe and elsewhere, a change in Italy’s nuclear plans will hardly be noticed. According to the German firm Siemans, at least 400 new reactors will be deployed globally by 2030. Moreover, several years ago Mr Vladimir Spidla, the Czech prime minister at the time, visited Finland, and among things he said that while Finland was the only country in Europe that displayed intentions to build an advanced nuclear facility, “soon almost all will join it.” They will join it if they prefer a higher standard of living to a lower standard! Italy’s energy situation is a great deal better than many because of its access to the natural gas of north Africa (and particularly the expanding reserves of Algeria), but as I never tire of pointing out, the first time I taught in Australia, the Maui gas field of New Zealand was thought by many to be virtually inexhaustible. In another decade however it may only be a memory. I can also mention that it was via the premature exhaustion of Maui resources that a misleading interpretation of New Zealand’s attempt to restructure its electric market was put into circulation – an interpretation that seduced several academic stars and ‘wannabes’ into supporting deregulation exercises that I correctly identified as economically absurd. Because of the ostensible “need” to rebuild its nuclear safety authority, and to identify sites for the new installations, the first new Italian reactor may not be in operation until 2020 – or even later. My reaction to this news is complete indifference! The important thing in Italy and elsewhere is that preparations are made to construct this equipment before the price of oil and gas goes into orbit, which many observers now believe could happen sooner rather than later. The nuclear reactors that are to be constructed in Italy are ‘European pressurized reactors (EPR)’, or as they are often designated ‘third generation’ (Gen 3) equipment, where the emphasis is on safety. (Safety with this equipment means that if control systems stop working, the reactor shuts down automatically, dissipates the heat produced by the reactions in its core, and stops both fuel and radioactive waste from escaping.) Unless I am mistaken, it makes sense for Italy not to hurry their new project, because while things might go smoothly if these reactors were being constructed in France, or even China, there could be problems of a cultural nature in Italy, where ENEL and EDF must coordinate their efforts in order to meet deadlines and keep costs under control. There have been some serious ‘issues’ of a cultural nature in Finland, where EDF and the Finnish power group TVO are constructing a 1600 MW(e) installation, that is the largest reactor in the world. Anne Lauvergeon – the CEO of Areva (France) – has blamed her Finnish collaborators for the delays and excessive costs experienced with this project, and without being especially familiar with the details of this accusation, I suspect that Madame Lauvergeon’s displeasure is justified. As compared to nuclear-friendly France, there are a large number of persons in Finland who believe that renewables are economically superior to nuclear, and even if this bizarre delusion has not infected the air in the vicinity of the construction site, it has almost certainly resulted in the kind of frictions that are unavoidable in multicultural projects – as I unfortunately discovered when teaching mathematical economics at a United Nations post-graduate institute in Senegal. With regard to the above comment of Prime Minister Spidla about the future of nuclear, I would like to emphasize that the basic issue is the growing but not well understood value of electricity in the life of persons in every country, in every walk of life, and especially individuals who are vulnerable to the economic discomforts that are likely to appear in a world characterized by a growing competition for resources and various other necessities. Naturally it is impossible to go into this matter in the present short communication, however as I have often stated, I choose to believe that a nuclear facility taking 4 years to construct, with a ‘life’ of at least 70 years, is (or will be) an optimal piece of equipment for delivering reliable and comparatively inexpensive electricity, and when lecturing I would not be happy to hear otherwise. On the other hand, I would be extremely happy if the new energy minister in the United States, Professor Chu, or one of his colleagues, would verify this contention, and make sure that this verification was circulated to every corner of the civilized world. On at least one occasion the former Swedish prime minister called nuclear energy “obsolete”, but unless I am mistaken he did so in hopes of obtaining the additional votes from members of the anti-nuclear booster club that would have enabled him to continue his presence at the head of the Swedish government. With all due respect, I am sure that in the overworked mind of that gentleman his gratuitous evaluation of nuclear’s future was to some extent justified, but in point of truth he was simply unable to comprehend the complex architecture of energy economics, and he is not alone where this shortcoming is concerned. As I suggested in a number of lectures, one of the recent prime ministers of Italy was deceived by the promise of plentiful and inexpensive natural gas due to trans-Mediterranean pipelines, but apparently the present prime minister does not agree, nor was it necessary for him to agree, because the price of gas will not have its present appeal to consumers for many more decades, or perhaps even years. (Although not certain, the price of natural gas is and has been for a long time below its equilibrium price, measured with respect to e.g. the BTU price of oil.) Though unfortunately ignored by many energy economists, the optimal course of action for a country like Italy may be maintaining or increasing its consumption of natural gas during the period in which entry – or re-entry – onto the nuclear scene is being prepared. Despite the opinion of deeply concerned though amateur economists like the former Swedish prime minister, if Italian and Swedish voters do not have a guaranteed access to nuclear energy later in this century, they could find themselves without access to the kind of goods and services that they have no desire or intention to be without – although as yet most of them do not appear to be inclined to recognize this fact.
11. CONCLUDING REMARKS
Let me sum up what I said in a recent article in the journal Energy and Environment (2004). We do not know if global warming is the real deal, or just part of a cycle; but we do know that gas and oil are running out, although it may take a few decades. In these circumstances the optimal behaviour is to get friendlier with the friendly atom, and do what Prime Minister Blair and the founder of Greenpeace suggest, which is to increase the use of nuclear energy. As suggested in this paper, that friendship will be necessary to supply the ‘extra energy’ needed to e.g. obtain the new fuels that voters in the energy importing countries have no intention of doing without, regardless of what they say. As Len Gould informed the forum EnergyPulse, these voters intend to have enough fuel to continue their transportation activities – much of which is mandatory if they are to maintain the standard of living of themselves and their families – even if they must go to war to obtain this commodity. Germany is a country that, together with Sweden, has expressed an intention to abandon its nuclear ambitions. After the widespread distribution of my short paper ‘Some Friendly Economics for the Nuclear Energy Booster Club’, I received mails from several persons in that country and elsewhere requesting their names to be removed from the list of persons directly receiving my papers. I was especially surprised by several of these ‘Dear Johns’, however… ‘Wir Werden Wiedermal Marschieren’ (=We Will March Again), was the title of a book that gained considerable attention in Germany when I was in that country with the U.S. Army. It became a best seller, and was about the retaking by the German Army of places like the Sudetenland (in Czechoslovakia) in the coming Third World War, which the author of that book and many of his readers saw as inevitable and necessary. Early in my ‘tour’, the armies of Nato countries participated in perhaps the largest peacetime military exercise ever held in ‘West’ Germany, which was called ‘Apple Harvest’. Toward the conclusion of that memorable exercise, the referees concluded that the Red Army had broken through the Fulda Gap and had almost reached Nuremberg, and it was judged that the only way that they could be stopped was with nuclear weapons. I had the opportunity to review the calculations for one of the simulated nuclear projectiles fired from a large cannon at the advancing Red Army. Had it been real instead of simulated, the eastern suburbs of Nuremberg would have been removed from the face of the earth. After that outcome came to be known, German officers, journalists, book-club members, politicians and various decision makers lost their appetite for marching. The same kind of reversion will eventually happen when the German public comes to realize that abandoning nuclear energy could wreak havoc on their standard of living! Among other things it could mean that virtually every factory in Germany becomes a candidate for transfer to parts of the world with an adequate and reliable supply of energy. This is the reason why I want the nuclear capacity in Sweden to increase. The key issue is not my choice of generating equipment but my pension! It is also the key issue for many of academics and energy professionals in this country and probably elsewhere, although they have been convinced by members of the anti-nuclear booster club and their favourite politicians that they would be doing themselves a disservice by understanding the easily understandable.
APPENDIX: A SHORT GLOSSARY Baseload Plant: This is a plant that is normally intended to take a large part of the load, and usually produces electricity at a constant or near constant rate, and is in operation continuously (as compared to a ‘peaking’ plant).
Boiling-Water Reactor: A light-water reactor in which water is used as both coolant and moderator, and in which water is allowed to boil in the core. This water produces steam that drives the turbine, to which an electric generator is attached.
Breeder Reactor: This is a reactor that consumes fissionable fuel, but at the same time produces more fuel than it consumes (due to its operating on the non-fissile component of its fuel). This operating process is called ‘breeding’.
Burnup: Avery important expression dealing with the amount of energy that can be produced per unit weight of fuel that is ‘burned’.
CANDU reactor: Essentially a Canadian reactor that uses heavy water or deuterium oxide rather than light water as the coolant and moderator.
Enrichment Taila Assay: A measure of the amount of fissile uranium remaining in the waste stream from the uranium enrichment process.
Fissile Material: Material that can be caused to undergo atomic fission when bombarded by neutrons. The most important are uranium-235, plutonium-239 and thorium.
Fission: The process whereby an atomic nucleus captures a neutron, and then splits into several nuclei – usually two – of lighter elements, releasing a considerable amount of energy and two or more neutrons.
Light-water reactor (LWR): A reactor that uses water as the primary coolant and moderator, with enriched uranium as fuel. The two types of LWRs are the boiling water reactor (BWR) and pressurised-water reactor (PWR).
MAGNOX Reactor: A gas-cooled reactor that uses graphite as the moderator and carbon dioxide as the coolant.
Natural Uranium: Uranium with the U-235 isotope present in a concentration of 0.711 percent by weight. The isotopic content here is exactly as it is found in nature. This can be compared with enriched uranium, which is uranium enriched in the isotope U-235 from 0.711 percent to at least 3 percent.
Nuclear Reactor: A device in which the nuclear fusion chain can be initiated, maintained and controlled so that the energy generated can be released at a specific rate.
Plutonium (Pu): A heavy, fissionable and radioactive metallic element, whose atomic number is 94. In occurs in nature in trace amounts, and in the present discussion is produced as a byproduct of the fission reaction in a uranium-fueled reactor.
Uranium Concentrate: A powder produced from naturally occurring uranium mineras as a result of milling uranium ores or the processing of uranium-bearing solutions. Synonymous with ‘yellowcake’ or Uranium Oxide. REFERENCES
Albouy, Michel (1986). Nouveau Instruments Financiers et Gestion du Couple Rentabilité Risque sur le Marché du Petrole. Stencil: Grenoble Université Banks, Ferdinand E. (2008). ‘The Political Economy of World Energy: An introductory Textbook’. Singapore, London and New York: World Scientific. ______. (2008). ‘Some friendly economics for the nuclear energy booster club’.EnergyPulse (www.EnergyPulse.net), (3.26.08). ______ . (2004). ‘A faith-based approach to global warming’, Energy and < Environment. Volume 15, Number 5: 837-852. _______. (2002). ‘Some aspects of nuclear energy and the Kyoto Protocol’. Geopolitics of Energy (July-August). ______. (2000). Energy Economics: A Modern Introduction. Dordrecht: Kluwer Academic Publishers. ______. (1985). The Political Economy of Coal. D.C. Heath & Co. (Lexington Books): Lexington and Toronto. Barre, Bertrand and Pierre-René Bauquis (2008), Understanding the Future Nuclear Power. Paris: Editions Hirlé. Beyer, Jim (2008). ’Comment on Banks’. EnergyPulse. (3.26.08). Braconnier, Fredrik (2005). Utsläpps rätter trissar upp redan högt elpris. Svenska Dagbladet (20 Aug). Carr, Donald E. (1976). Energy and the Earth Machine. London: Abacus. Constanty, H. (1995). “Nucleaire: le grand trouble” L’Expansion (68-73). Duffin, Murray (2004). The energy challenge 2004 – nuclear’. EnergyPulse. www.EnergyPulse.net (10.8.04). Einhorn, Michael (1983). ‘Optimal systems planning with fuel shortages and emissions constraints’. The Energy Journal (April). Goodstein, David (2005). Out of Gas: The End of the Age of Oil. New York: Norton. Gould, Len (2008). ‘Comment on Banks’. EnergyPulse, (3-26-08) Grunwald, Michael (2008). ‘The clean energy scam’. Time (April 14). Guentcheva, D. and J. Vira (1984). ‘Economics of nuclear versus coal’. Energy Policy (December). Harlinger, Hildegard (1975). Neue Modelle für die Zukunft der Menshheit. IFO Institute für Wirtschaftsforschung. Munich. Hanlon, Michael (2005) ‘Why do greens hate machines’. The Spectator(6 August). Held, C.M. (1983). ‘Evolution of size-scaling effects on electricity production during the l970s’. Presented at the Atomic Energy Agency, Vienna. Hopf, James (2008). ’Comment on Banks’. EnergyPulse (3.26-08). Kok, Kenneth (2008). ’Comment on Banks’. EnergyPulse. (3.26.08). ______ . (2008). ’Vision for the development of an international nuclear fuel recycling program’. Paper presented at the 11th International Conference on Environmental Remediation and Radioactive Waste Management. Bruges Belgium (September 2 – 6). Kullander, Sven, Henning Rodhe, Mats Marms-Ringdahl, and Dick Hedberg (2002). ’Okunnig att avveckla kärnkraften’. Dagens Nyheter (7 April). Matsui, Ken-Ichi (1998). ’Global demand growth of power generation’. The Energy Journal (No.2). Martin, J-M. (1992). Economie et Politique de L’energie. Paris:Armand Co Michel, Jeffrey H. (2008). ‘German lignite usage: expensive and unsustainable’.Acid News (www.acidrain.org). Nordhaus, William D. (1973). ‘The allocation of energy resources’. Brookings Papers , No 3. Ogg, Clay (2008). ‘Environmental challenges associated with corn ethanol Production’. Geopolitics of Energy (January). Owen, Anthony David (1985). The Economics of Uranium. New York: Praeger . Rhodes, Richard and Denis Beller (2000), ‘The need for nuclear power’. Foreign Affairs (January-February) Romm, Joseph J. and Amory B. Lovins (1992). ‘Fueling a competitive Economy’. Foreign Affairs (Winter). Roques, Fabien and William J Nuttall, David Newbery, Richard de Neufville, Stephen Connors, (2006), ‘Nuclear power: a hedge against undertain gas and carbon Prices’. The Energy Journal (No. 4). Rose, Johanna (1998). “Nya Krafter”, Forskning och Framsteg (September). Schurr, S.H. (1984).‘Energy use, technological change, and productive efficiency: an economic-historical interpretation’. Annual Review of Energy. Scire, John and Ricardo Lopez (2008). ‘Yucca Mountain: Plan C’. The Nevada Appeal (Carson City, Nevada). Schlageter, David (2008). ‘Comment on Alan Caruba (‘Congress conjures up an energy deficit’). (www.energypulse.net) (Feb. 6, 2008). Somsel, Joseph (2008). ‘Comment on Banks’. EnergyPulse (4.8.08). Stipp, David (2004). ‘Climate collapse’. Fortune (February 9). Tanguy, Pierre (1997). Nucléaire: Pas de Panique. Paris: Editions Nucléon. Thunell, J. (1979). Kol, Olja, Kärnkraft –en Jamförelse. Stockholm: Ingenjörsförlagen.Yarrow, George (1988). ‘Nuclear Power’. Economic Policy (April).
Professor Ferdinand E. Banks May 28th, 2009 ferdinand.banks@telia.com
|
| Home :: Archives :: Contact |
SUNDAY EDITION December 28th, 2025 © 2025 321energy.com |
|